Dear B. Turneabe,
Thanks for your post. I am not updating things as much as I would like to. Ok, I didn’t get what was missing, the triangular ones. I’ll do it when I find a few minutes nearby my tabletPC (too long to do it with the mouse).
As for the number of threads, I have done this page but it’s in French. To make a long story short, the number of threads in a rectangular plate is the greatest common divisor of the width and the height. For example 6x9 will give you 3 threads because 6=3x2 and 9=3x3, the common divisor is 3.
For other designs, it is more complicated. But there are some tricks:
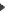 Put a wall where 2 different threads cross to merge them into one.
Put a wall where 2 different threads cross to merge them into one.
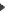 Change a wall between 2 different threads will merge them into one, whether you flip the wall or you change it into a crossing.
Change a wall between 2 different threads will merge them into one, whether you flip the wall or you change it into a crossing.
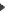 When one thread is self-crossing, one of the two types of wall will split it into two threads.
When one thread is self-crossing, one of the two types of wall will split it into two threads.
This way, with little tweaks here and there, you can achieve whichever number of threads you want.
Best regards, Christian
Reply to this message
 Take this a a collection of patterns, put together, it is not supposed to look nice as a whole.
Take this a a collection of patterns, put together, it is not supposed to look nice as a whole. before looking at the answer, or a more sophisticated one:
before looking at the answer, or a more sophisticated one:
 and its solution.
and its solution. and try to discover new patterns that you like.
and try to discover new patterns that you like.