In diesem Kapitel werden Sie lernen, ein Motiv so in einen Rahmen zu setzen, dass Sie es in ein größeres Bild einfügen können. Lassen Sie mich an einem Beispiel zeigen, wozu das notwendig ist.
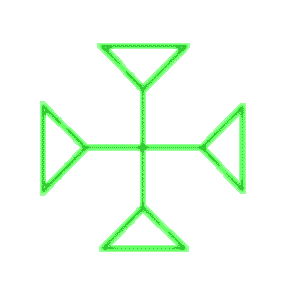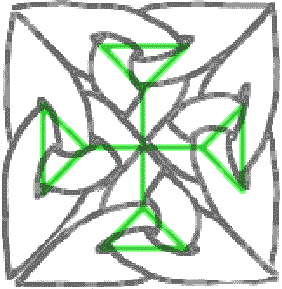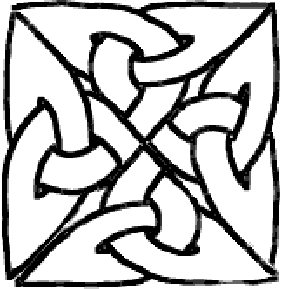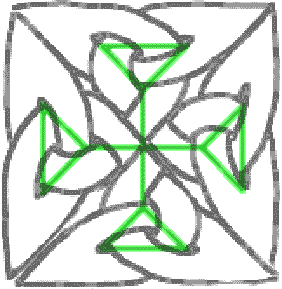
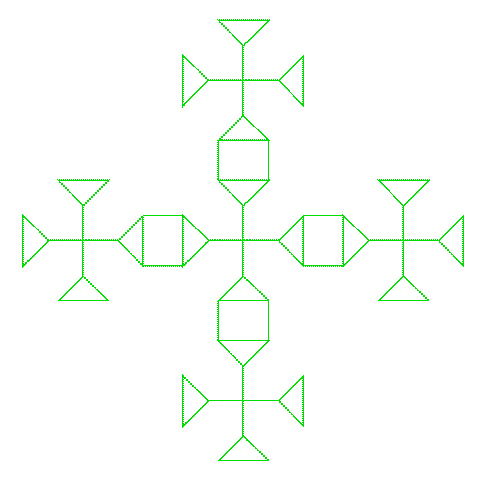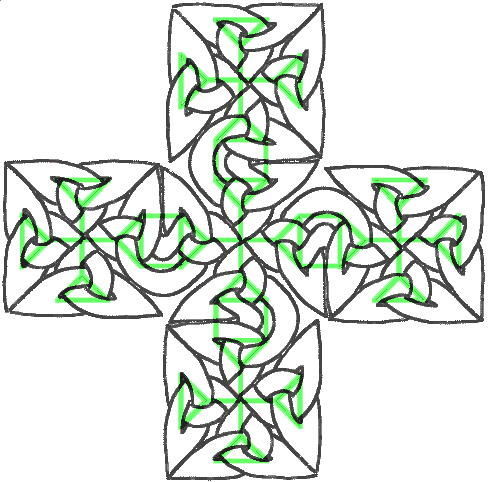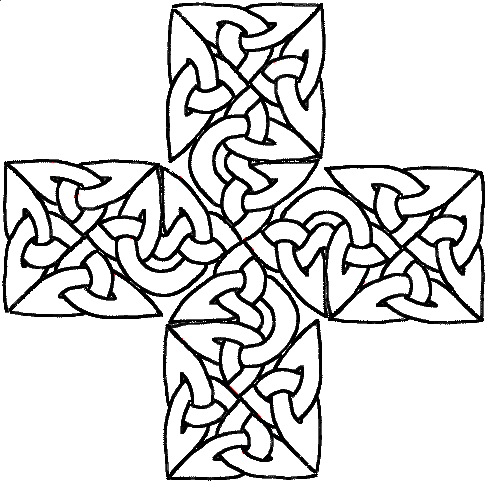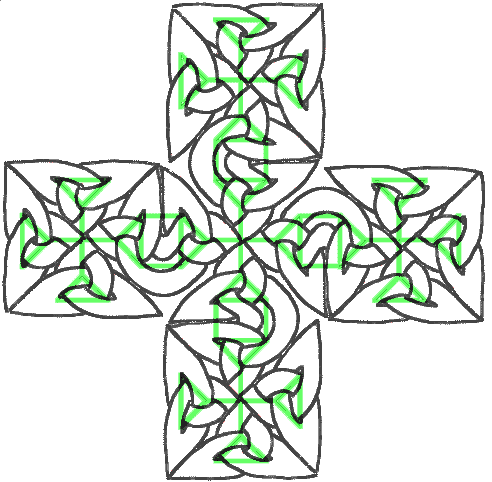
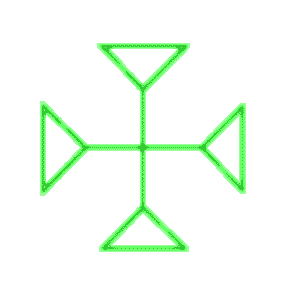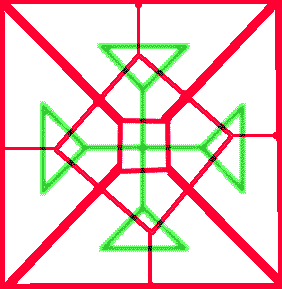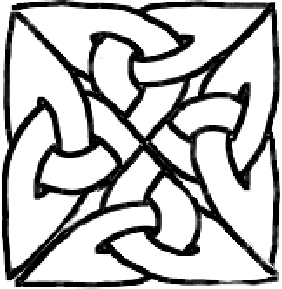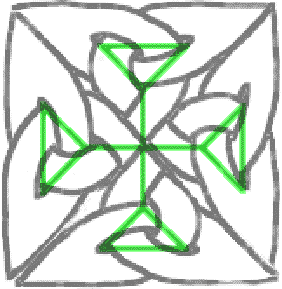
Nehmen wir an, Sie mögen - so wie ich - den Kleeblattknoten, und Sie wollen daraus etwas machen. Zum Beispiel ein Kreuz. Da das Kleeblatt auf einem Dreieck beruht, werden Sie versuchen, vier Dreiecke zusammenzusetzen. Mit viel Mühe und Schweiß kommen Sie vielleicht zu folgendem Ergebnis:
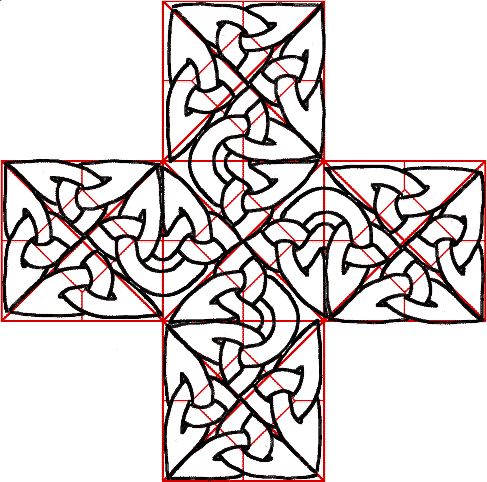
Das ist schon sehr schön, aber da müssen wir noch was dran machen. Sie können versuchen, weiter zu gehen und aus diesem Motiv ein noch größeres Kreuz machen. Unter viel Stöhnen und Schimpfen erhalten Sie möglicherweise folgendes:
Sehr schön, aber schwer zu verwenden. Sie können es ja versuchen, werden aber merken, dass Sie auf diese Weise kein großes und genaues Bild zustande bekommen. Zum Glück gibt es eine andere Methode, eben das Einrahmen. Dafür müssen Sie jedoch zuerst einen einfachen aber inhaltsreichen mathematischen Begriff verstanden haben:
Dualität
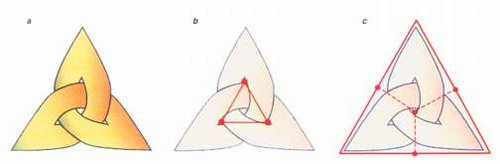
Nehmen wir noch einmal den Kleeblattknoten. Wenn Sie davon das Gitter herausarbeiten (extrahieren), setzen Sie die Eckpunkte jetzt nicht in die weißen, sondern in die schwarzen Flächen. Natürlich ist es mit der äußeren Fläche etwas Besonderes: hier werden die Eckpunkte, die nah an die Überkreuzungen gesetzt werden, miteinander durch eine durchgehende Wand, die das ganze Motiv einrahmt, verbunden. Als Bild erhält man anstelle der Figur b die Figur c:
Was Sie jetzt gesehen haben, ist die Konstruktion des Duals zum Dreieck. Wenn Sie einmal den Graphen haben, brauchen Sie den Knoten gar nicht mehr, sondern Sie können sein Dual direkt konstruieren: die Eckpunkte des Duals liegen in den Mittelpunkten der Flächen des Ausgangsgraphen und seine Seiten liegen quer zu jeder Ausgangsseite:
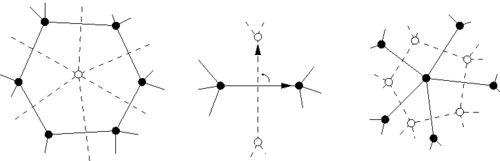
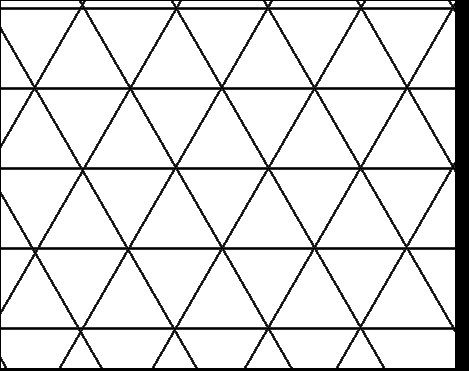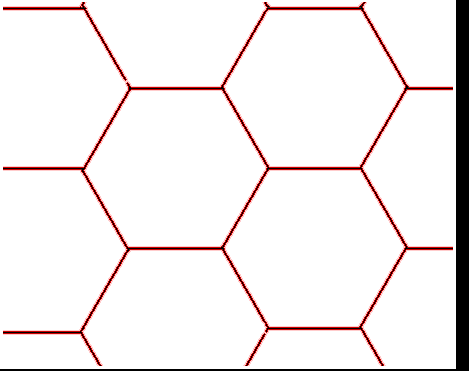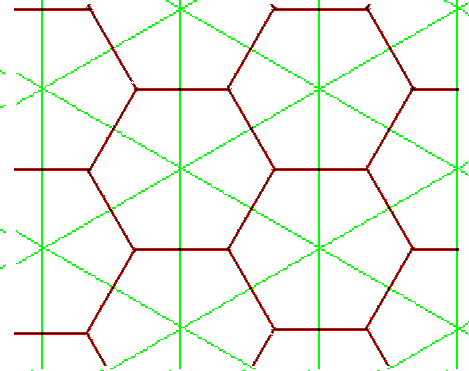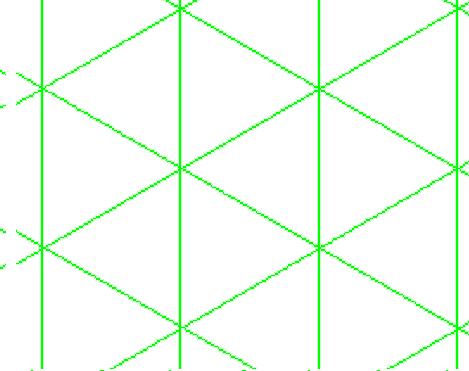
Zum Beispiel sind das Dreiecks- und das Sechsecksgitter dual zueinander. Das Dual eines Dreiecks ist ein Teil des Sechsecksgitters.
Sie sehen jetzt, da unser Kleeblattknoten in einem Rahmen sitzt, dass es sehr einfach ist, daraus ein Kreuz zu machen. Sie zeichnen nur ein Quadrat mit seinen Diagonalen, wodurch Sie vier Dreiecke erhalten, zeichnen das Dualmotiv des Kleeblattknotens in jedes Dreieck und öffnen ein paar Wände, so dass die verschiedenen Knoten zu einem werden. Im Bild ausgedrückt:
Mit dem großen Kreuz ist es noch einfacher. Zeichnen Sie fünf solcher Quadrate zusammen und öffnen Sie ein paar Wände, damit die kleinen Kreuze ineinander übergehen:
Die Idee dahinter ist, dass man erst kleine Knoten sucht, die einem gefallen, aus diesen den Dual-Graphen entwickelt und in einen Rahmen setzt und mit diesen Rahmen die zu gestaltende Fläche pflastert, um ein großes Bild zu erhalten.
Hier ein weiteres Beispiel. Wenn Sie mit Dreiecksgittern herumspielen, stoßen Sie auch auf dieses hübsche Motiv:
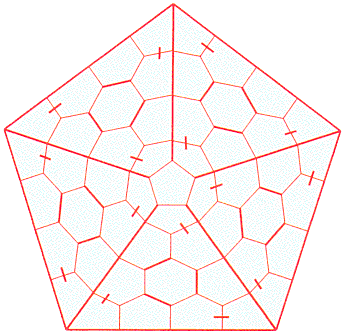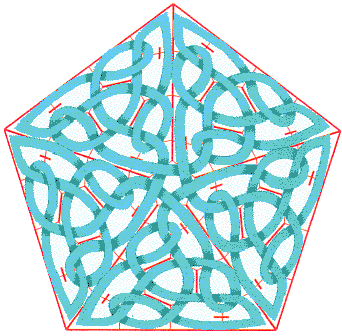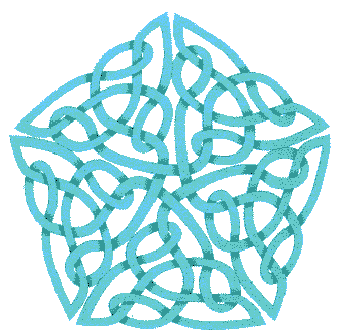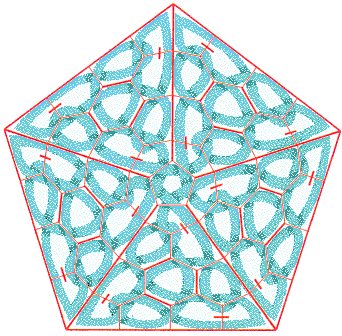
Um daraus etwas zu machen, müssen Sie erst dessen Dual-Graph herausarbeiten:
Daraus lässt sich zum Beispiel ein fünfseitiges Motiv machen:
Die einzige Schwierigkeit besteht in der Wahl der Wände, die Sie in den umgebenden Dreiecksrahmen öffnen. Es müssen genügend sein, damit die Knoten ineinander übergehen, und dabei so platziert, dass man jedes Motiv wiedererkennt. Das ist wie bei einer guten Ehe: ein Ganzes werden bei Wahrung der Individualität
Wenn Sie jetzt Knoten und Flechtwerke haben wollen, die ein Anfang und ein Ende haben, sollten Sie einen Blick auf Verflechtungen.