Nesta seção, você vai aprender a colocar um pequeno nó agradável em uma caixa, o que eu chamo de "encapsulamento". Baseia-se numa noção matemática chamada "dualidade", mas pare! Não fuja, é mais fácil começar com um exemplo para mostrar que 1. é fácil; 2. Você realmente precisa disso se quiser fazer algo grande no negócio do nó celta.
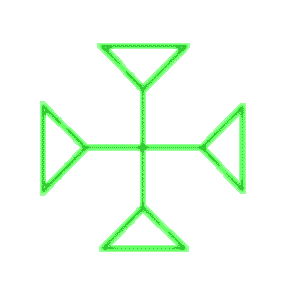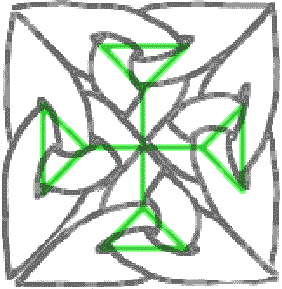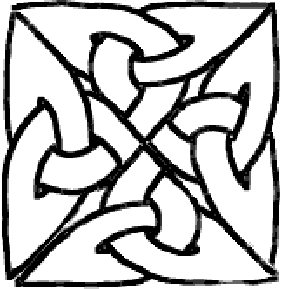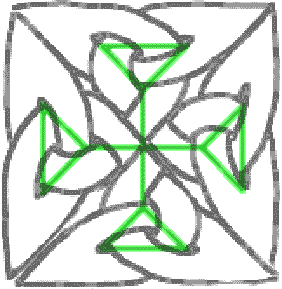
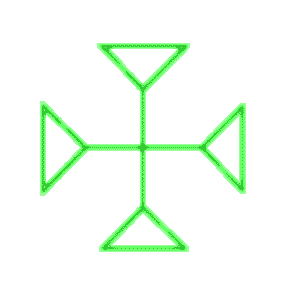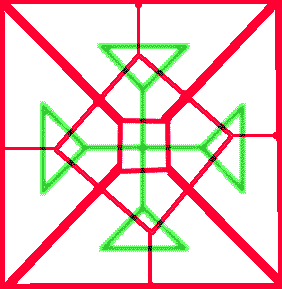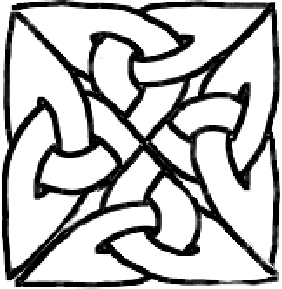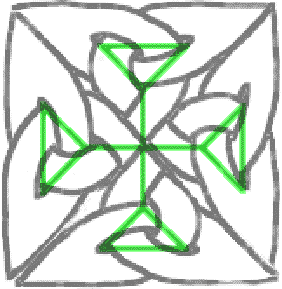
Suponha que você goste do nó trevo (eu faço!) E você quer fazer algo com ele. Por exemplo, uma cruz. Como o trevo é codificado por um triângulo, você tenta colocar quatro triângulos juntos. Depois de muito suor, maldições e erros, você acaba com algo assim:
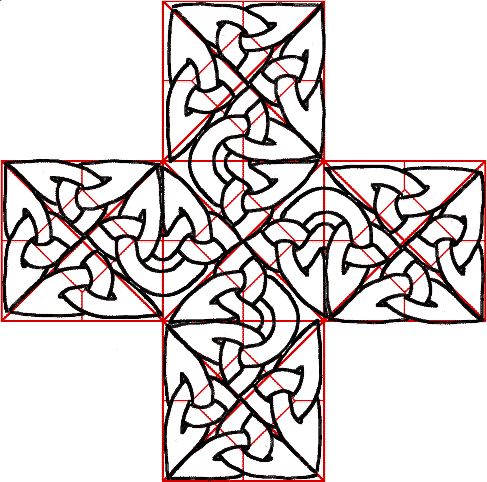
Isso é muito bom, mas exige muito ajuste manual. Você pode tentar ir mais longe e fazer uma cruz maior com cinco dessas pequenas cruzes. Depois de muitas palavras feias, você pode obter algo como isto:
Muito bom, mas difícil de ajustar, não é? Se você tentou, percebeu que não pode fazer figuras grandes e precisas dessa maneira. Felizmente, há outra maneira, é chamado encapsulamento. Mas primeiro você tem que aprender coisas sobre uma noção matemática (não fuja!):
Dualidade
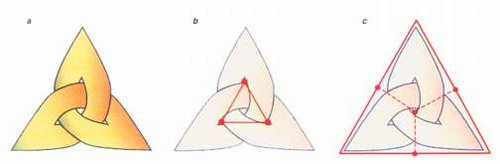
Voltando ao trevo, suponha que, quando você extraia seu gráfico, você não coloca os vértices no branco, mas nas regiões pretas (veja Extração). Claro, a região infinita tem que ser dividida em vários vértices não apenas um e esses vértices são simbolicamente fundidos em conjunto por uma parede contínua que circunda todo o nó. Em imagens em vez de palavras, você acabaria com a figura c, não figura b:
O que você acabou de testemunhar é a construção do gráfico dual do triângulo. Depois de ter o gráfico, você não precisa do nó, você pode construir seu dual de imediato: os vértices do gráfico dual estão no meio das faces do gráfico original e suas arestas são transversais a cada aresta primal:
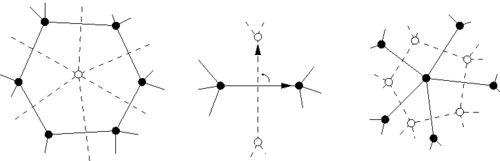
Por exemplo, as redes triangulares e hexagonais são duais entre si. O dual de um triângulo é uma porção da rede hexagonal.
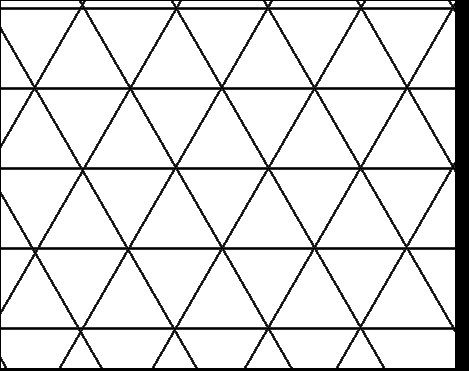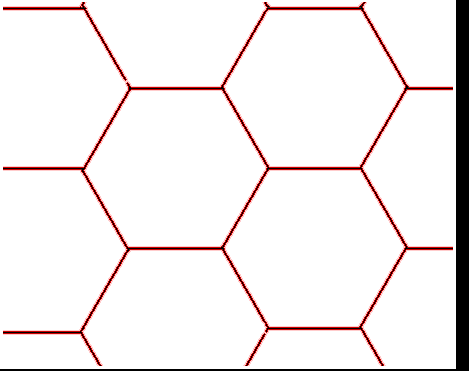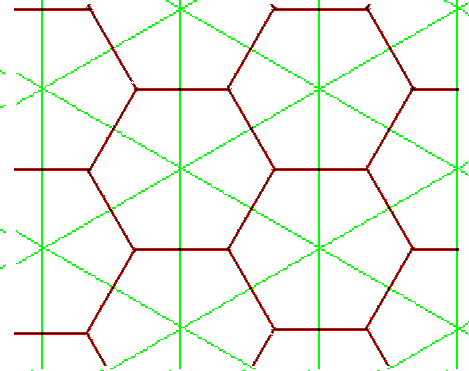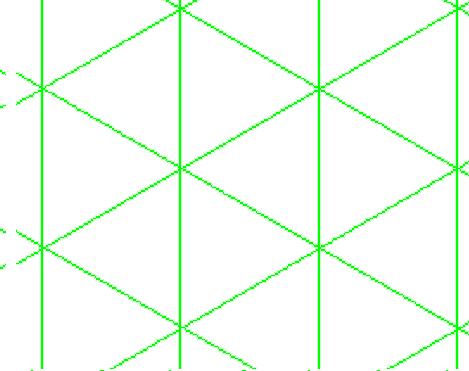
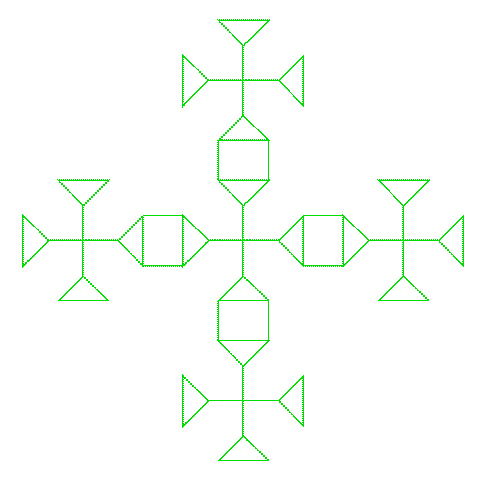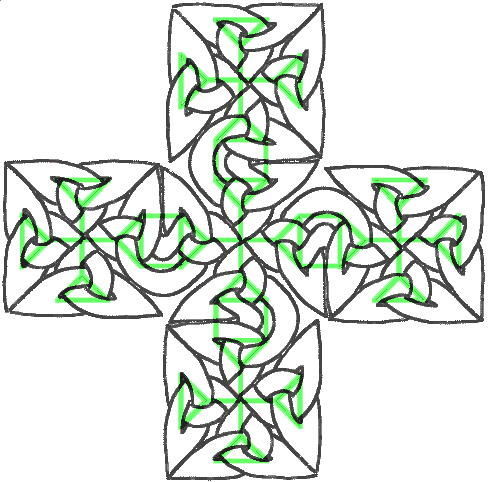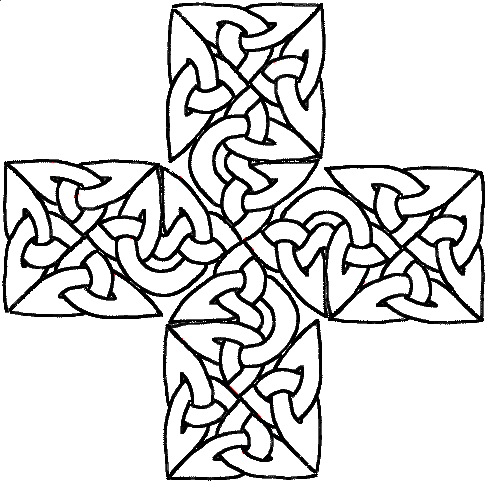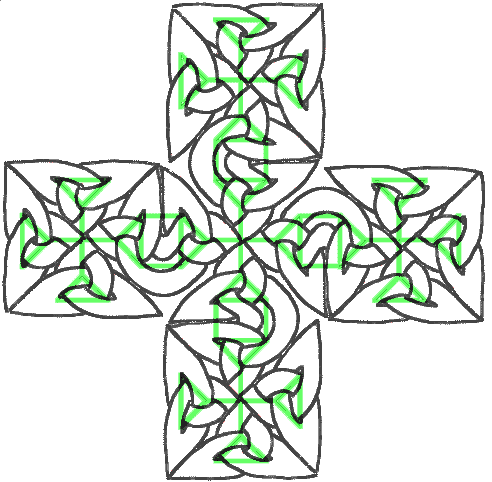
Agora você vê que é mais fácil formar uma pequena cruz usando o gráfico dual, o nó é completado dentro de uma caixa, uma cápsula triangular! Você simplesmente desenhou um quadrado, adicione suas duas diagonais para fazer quatro triângulos, copie o motivo dual dentro de cada triângulo e abra algumas arestas nas paredes para que os trevos se fundam em um. Em imagens:
E é ainda mais fácil construir a maior cruz, simplesmente empilhar cinco quadrados, como aquele e abrir algumas portas para deixá-los escapar de suas caixas:
Então, a filosofia é que, para fazer um grande trabalho, primeiro você precisa encontrar pequenos nós que você gosta, elaborar seu gráfico dual que está incluído em uma cápsula e usar essas caixas para marcar a área que deseja projetar. Vamos dar uma olhada em outro exemplo. Jogando com redes triangulares, você tropeçou nesse motivo agradável:

Para fazer algo com ele, primeiro você precisa descobrir seu gráfico dual:
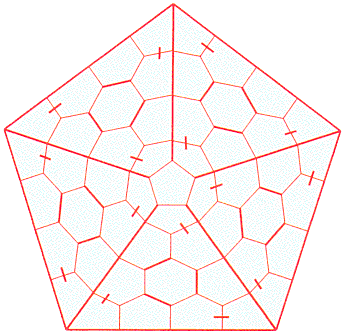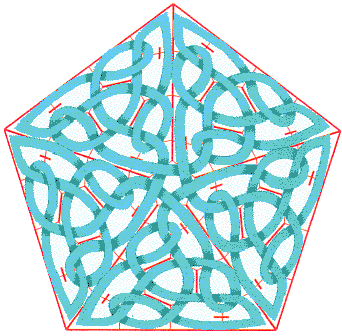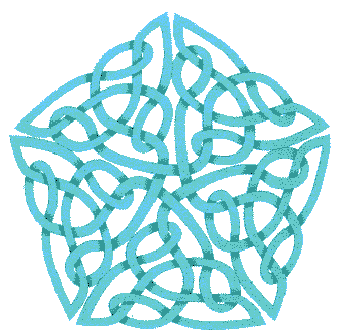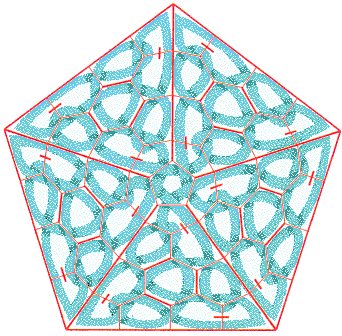
Então você pode fazer, por exemplo, uma estrela cinco ramificada:
Agora, se você quer fazer nós que tenham um começo e um fim, você deve procurar enredos.